To link historical census records at the individual level, I have to compare names across sources. These names are often recorded with error (or transcribed with error or digitized with error or just changed over time) so the merging of census micro data is far from trivial. I describe a lot of this work in my record linkage paper. One tool I use to compare records is string distance. Specifically, I use the Jaro-Winkler distance. I’ve written a Stata ado file to implement Jaro-Winkler, but in R I use the Jaro-Winkler method in the stringdist package.

Today I was thinking about ways to speed up my census record linkage procedures. In particular, I thought I might be able to optimize the string comparison. I like Jaro-Winkler for a lot of reasons. For one, it penalizes differences early in strings more than later in strings which—I think—makes sense for names. But could I get better (or quicker) results with another string comparison method? There are a number built in to the stringdist package so I tried them all.

library(data.table)
library(magrittr)
library(stringr)
library(stringdist)
library(microbenchmark)
library(ggplot2)

source("~/Dropbox/Research/.Rprofile")

After loading the libraries I need, I also pulled in a list of first names I’ve compiled from various sources (I’ll post about that at a later time but the goal is to build a massive first name to nick name to alternative name database to aid in record linkage).

# load the firstname database
fn_db <- fread("~/Dropbox/Research/_knowledgebase/censuslink/out/fn_links_men_5.csv") %>% unique()

The fn_db (firstname database) has 39419 observations so I sample just 500 from it and create a 250 thousand row datatable comparing each name to each other name.

K <- 500
fn <- fn_db[sample(.N, K)] %>%
  .[, list(id = 1, name1)] %>%
  merge(., ., by = "id", allow.cartesian = TRUE) %>%
  .[, id := NULL] %>%
  setnames(c("name1", "name2"))

Then, I use the microbenchmark package and (100 times) calculate each of the string distances:

reps <- 1e2
strdist_speed <-
  microbenchmark(
    fn[, osa := stringdist(name1, name2, method = "osa")],
    fn[, lv := stringdist(name1, name2, method = "lv")],
    fn[, dl := stringdist(name1, name2, method = "dl")],
    fn[, hamming := stringdist(name1, name2, method = "hamming")],
    fn[, lcs := stringdist(name1, name2, method = "lcs")],
    fn[, qgram := stringdist(name1, name2, method = "qgram")],
    fn[, cosine := stringdist(name1, name2, method = "cosine")],
    fn[, jaccard := stringdist(name1, name2, method = "jaccard")],
    fn[, jw := stringdist(name1, name2, method = "jw", p = 0.1)],
    fn[, jaro := stringdist(name1, name2, method = "jw", p = 0)],
    times = reps
  ) %>%
  as.data.table() %>%
  .[, funct := str_extract(expr, '\\`\\(.*, s.?') %>% str_replace("\\`\\(", "") %>% str_replace(", st", "")] %>%
  .[, time := time * 1e-6]

Which methods are the fastest?

ggplot(strdist_speed, aes(y = time, x = funct)) +
  geom_jitter(height = 0, width = 0.1, alpha = .1) +
  xlab("method") + ylab("seconds") +
  scale_y_log10() +
  theme_jjf()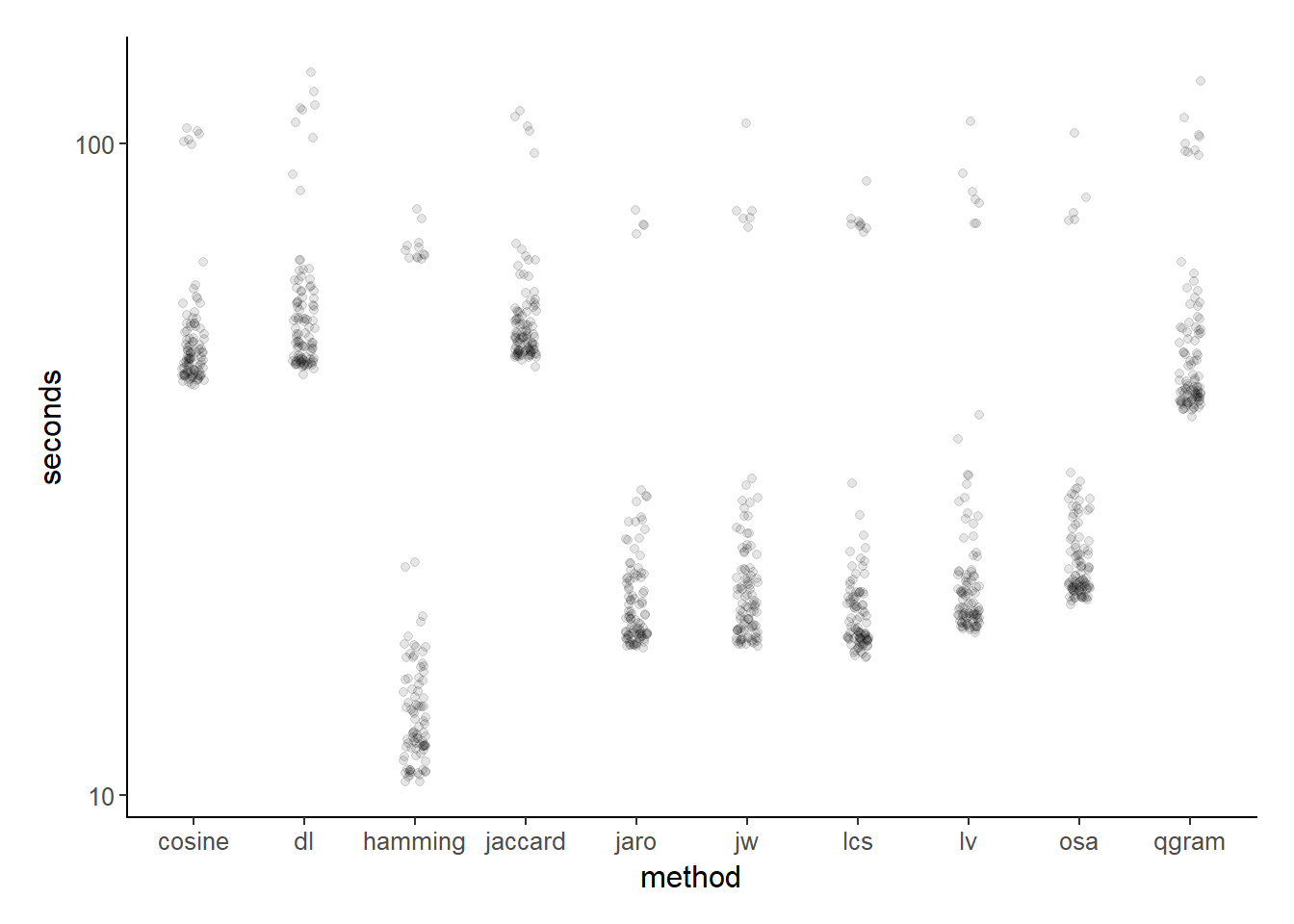

(Yes, I have my own custom theme for ggplot(). I’ll talk about that another time.)

The fastest method appears to be the hamming distance. But, a quick look at the definition of the hamming distance suggests that it is totally unsuitable for my purposes. Per wikipedia:

In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of substitutions required to change one string into the other, or the minimum number of errors that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences.

The problem is in the first sentence: “strings of equal length”. While names are all short strings, they are certainly not uniformly distributed in length.

ggplot(fn_db, aes(x = nchar(name1) %>% as.factor())) +
  geom_histogram(stat = "count") +
  xlab("First Name Character Length") +
  theme_jjf()

## Warning: Ignoring unknown parameters: binwidth, bins, pad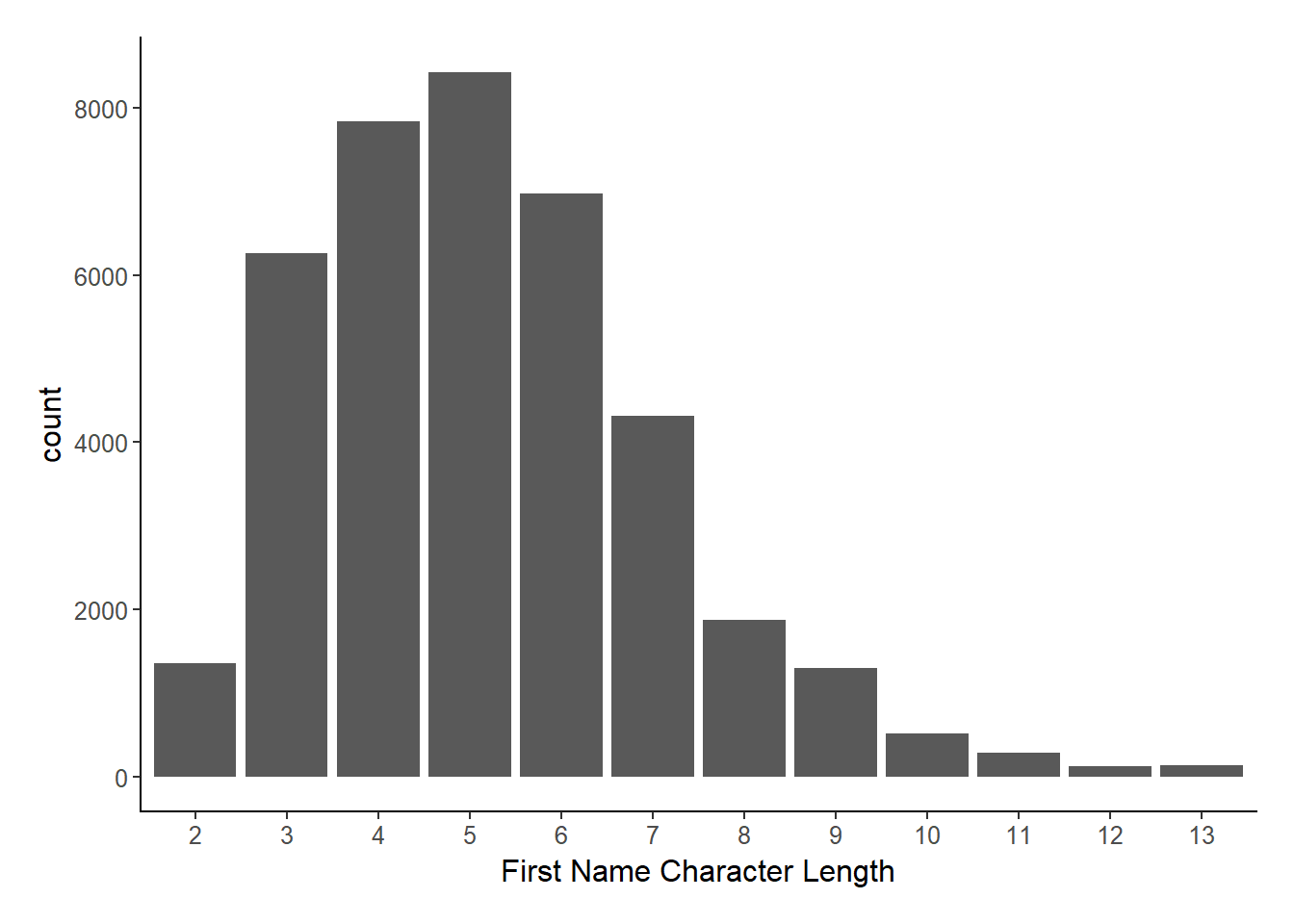

Because so many string pairs are not the same length, of course the hamming distance is fast!

So, other than hamming distance, what are the quickest string distance metrics? Well, though this is the first time I’ve thought about optimization of string distance for record linkage, I was right all along. Along with the original Jaro distance, lcs (Longest common substring distance), lv (the Levenshtein distance), and osa (optimal string alignment), Jaro-Winkler is at the top of the pile. Given that I already like JW distance for other reasons and that I already use it, looks like I’ll stick with it.